With the basic engine created, the next step is adding a couple of basic non-RL agents.

The heuristic agent

The first agent will follow a simple heuristic: make the most central move possible. For this, I wrote this prompt:

Add a new “heuristic” agent. The agent:

if it has a winning move, it plays it

if the opponent has one winning move, it blocks it

if a move gives the opponent a winning move, it avoids it

for the rest of the cases, it prioritices central moves, the more in the center the better

for ties, choose a random move

It implements it without a hitch. I test it against the random agent, playing the heuristic as the second player:

Running 1000 games: Random vs Heuristic

 100/1000 games completed
 200/1000 games completed
 300/1000 games completed
 400/1000 games completed
 500/1000 games completed
 600/1000 games completed
 700/1000 games completed
 800/1000 games completed
 900/1000 games completed
 1000/1000 games completed

========================================
Results
========================================

Random (Player 1):
 Wins:     13 (  1.3%)

Heuristic (Player 2):
 Wins:    987 ( 98.7%)

Draws:        0 (  0.0%)

Total:     1000 games
========================================

That simple rule makes all the difference, and all of a sudden, playing randomly is an almost sure defeat.

The minimax agent

I (vibe)coded the heuristic agent in January, but I didn’t continue the post until February, when the new Claude Opus 4.6 and GPT-5.3-Codex were simultaneously released. So the new code comes from these two models (mostly GPT).

My next prompt:

Add a minimax agent to use as baseline for future Q-Learning agents (like the heuristic agent)

Minimax is an algorithm that can be used in two-player games with perfect information. The basic idea is to build a tree with all possible moves. If I’m the first player (the maximizer), at the beginning of the game, the board is empty, and that is the root of the tree.

From there, we get seven edges, one for one of my possible moves, that end in nodes corresponding to the state of the board after that move (a piece at the bottom of the selected column). From each node grow seven edges with the possible moves of my opponent (the minimizer), and so on.

This calculation repeats until all edges get to a terminal state (win, lose, or draw), or we get to a predefined evaluation limit (we can build the whole tree because it is computationally too expensive)

Once we have the tree, we compute a score for each leaf (the terminal nodes), and we choose one of them: if the edges getting to the nodes correspond to moves for the adversary (minimizer nodes), we choose the lowest score, if to my moves (maximizer nodes), we choose the highest one. The reason is that we’ll compute the score so that the higher the score, the better for the maximizer player, and we assume the minizer we’ll choose the move we evaluate as the worst for us.

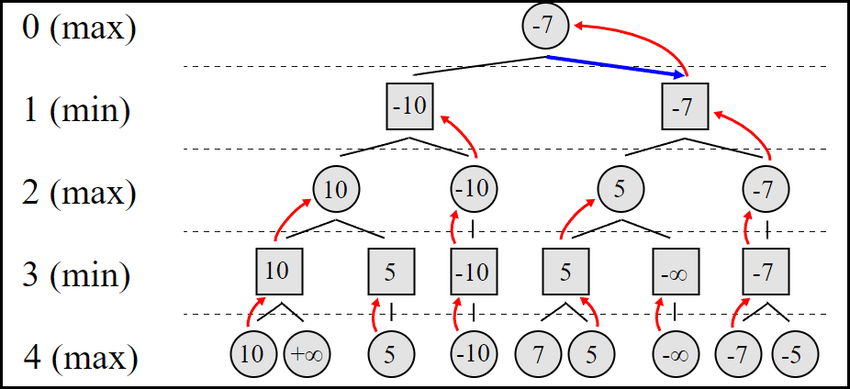
And how do we compute the score? We also use a heuristic for this. The one Codex chose (the idea seems logical, the detail may be suboptimal, or maybe not) is to add points based on how many pieces in a row you have, with an additional score based on how central your pieces are. This is how Claude explains the evaluation function:

The application lets you choose the depth of the tree, four by default. It works, but it is a little slow. I imagine that I should be using all 24 cores for this, so I prompted Codex again:

Make the benchmark.py script multithreaded so it can run several games at the same time

When I tried the first implementation, the result was way worse than the single-thread version. So I tried again:

There is some problem with the multithreading. Now the execution takes way longer. Anaylize the code with detail and identify the issues.

It finally creates a multithreaded version that improves speed.

The Minimax agent beats the heuristic, although not for that much:

Select Player 1 (X):

 1. Random
 2. Heuristic
 3. Minimax

Enter choice: 2

Select Player 2 (O):

 1. Random
 2. Heuristic
 3. Minimax

Enter choice: 3
Select Player 2 (O) minimax depth [4]:

Number of games [1000]: 10000
Workers [24]:

Running 10000 games on 24 workers: Heuristic vs Minimax(d=4)

 4800/10000 games completed
 7400/10000 games completed
 10000/10000 games completed

========================================
Results
========================================

Heuristic (Player 1):
 Wins:   3904 ( 39.0%)

Minimax(d=4) (Player 2):
 Wins:   4818 ( 48.2%)

Draws:     1278 ( 12.8%)

Total:    10000 games
========================================

This version of the code is here.